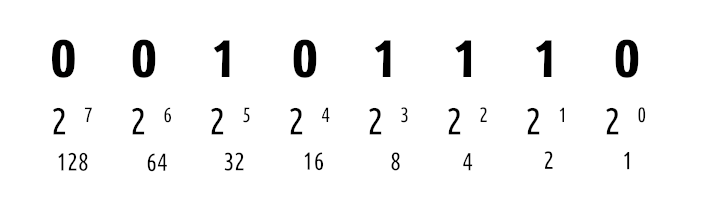Speaking the Language of the Computer

What is a computer?

In brief, a computer is an general purpose electronic machine made to manipulate the flow of electricity to perform programmed tasks. Without getting too much into the nitty gritty of the hardware engineering, the computer can be thought of a incredibly complex, deterministic system of layered logic gates.

At the most basic level, electricity has two states which the computer can use to perform tasks: ON and OFF. Simple! Either electricity is flowing, or it is not.

But how do we make this useful for humans?

Some of the earliest forms of computers (monstrous, analog, mechanical machines) were made to do just what the name implies: compute; that is, take numbers n and do something with them mathematically.

Around the time that computers were just beginning to transition from analog to digital, we found that binary numbers (or numbers in base-2) from mathematics are incredibly useful for representing mathematical data for humans, since the flow of electricity only has two states, represented as 0 (OFF) and 1 (ON).

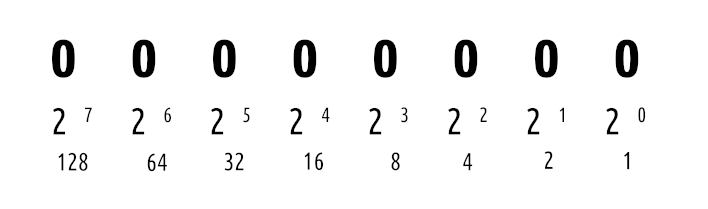
The below number is a representational “byte” of information, consisting of 8 binary digits, or “bits“:

In the above example, all one has to do to get a number between 256 and 0, would be to “flip” the bits. For example, the following number is “46” in binary:

Now, mind you, this is the simplest way to represent data on a computer, but as the numbers increase, this method of representing data can get unwieldy and difficult for humans to parse. Alas, some brilliant mind somewhere along the line found that you can translate binary into hexidecimal (base-16, in other words) pretty easily!

To represent numbers as hexidecimal, you use the following characters to represent the numbers 0-15 in decimal (base-10):

0 = 0
1 = 1
2 = 2
3 = 3
4 = 4
5 = 5
6 = 6
7 = 7
8 = 8
9 = 9
A = 10
B = 11
C = 12
D = 13
E = 14
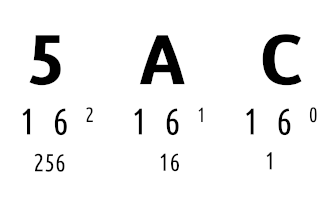
F = 15

You can think of base-16 numbers as having 16 states, instead of the 2 states of base-2 numbers. One of the benefits of using hexidecimal numbers over binary numbers is that you can represent extremely large numbers with very few characters, which can make information much easier to parse. Let’s demonstrate, with just 3 numbers of hex. The following number is “1452“(base-10) in hex:

For comparison, you would need 12 bits to get the same number. Additionally, converting from binary to hexidecimal and back is nearly trivial if the binary is broken into 4 bit segments, each adding up to a total of 15:

C = 12 = 1011
A = 10 = 1010
5 = 5 = (0)101

0101 1010 1011 = (0)10110101011

Armed with this information, we can begin to see how humans can begin to read and parse what’s referred to as “machine code”. But what if I wanted to do other things, like simple word processing or decimal math? There’s nothing in machine code that tells the computer that I want an “A” or a “Z”! I can’t use punctuation, and I don’t want to have to type out a number in binary anytime I need to perform math. I only have numbers that represent instructions that the computer follows. What do I do?

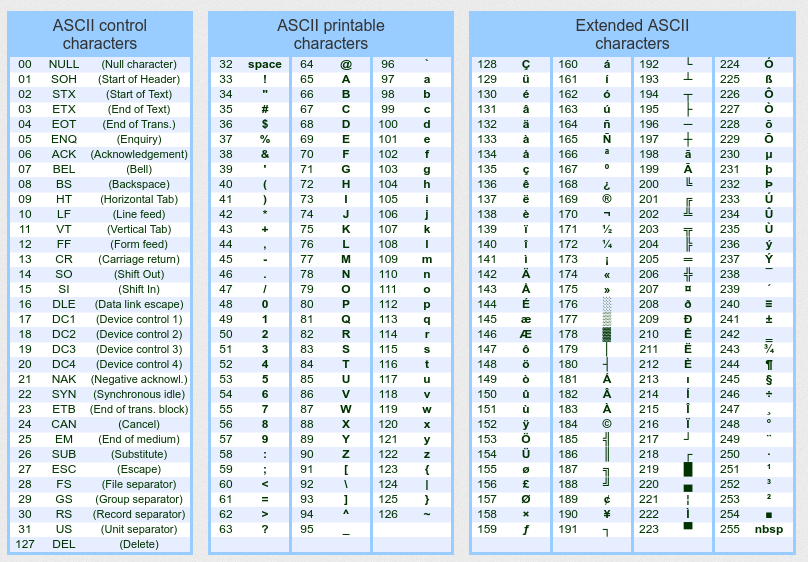
Well, here enters character encoding, and the American Standard Code for Information Interchange (or ASCII, as it’s known).

ASCII allows people to abstract themselves away from the machine code by telling the computer that specific arrangements of binary numbers (and hex, by extension) represent letters, decimal numbers, punctuation, etc. It is also a standard for most computers, so that they are able to communicate to one another effectively.

Putting all of this together, we can start to piece together ways in which we can begin to to talk to the computer in meaningful ways.